建议麦当劳。

最近经常说这句话。发现，在很多时候麦当劳都是几个人聚餐的最优解：

• 可能有回民
• 可能有人不吃辣、醋
• 可能有人不吃鱼羊海鲜

绝大部分情况下，麦当劳都覆盖了至少一部分一个人爱吃的东西。因此，本站的description改成：

建议麦当劳。

PS: 发现过去一年我吃了至少5000元的麦当劳。

背景

最近在校内部署了我们开发的EduOJ以供数据结构与算法课程使用。OJ中使用了 clang 编译器以避免gcc编译器造成的坑（如#include</dev/random>能卡死编译器，以及某段很短的代码能产生数G的错误日志）。同时，按照惯例，开启了O2优化。

上线后不久，很多同学反映说OJ不好用。我问咋回事儿，同学说代码本地运行都是对的，提交到平台上之后就是错的了。相关代码片段如下：

1. 这段代码运行结果和本地不一样

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

while (head->next != nullptr) {
  if (cnt == m) {
    cout << p->data << ' ';
      
    // del 是代码作者定义的一个函数，里面调用了
    // delete p
    del(p); 
    cnt = 0;
  } else {
    cnt += 1;
    if (p->next != nullptr) {
      p = p->next;
    } else {
      p = head->next;
    }
  }
}

可以看到，他在delete p后还访问了p->next。

2. 这段更离谱：

1
2
3
4
5
6
7
8

template<typename T> bool ArrayList<T>::append(T const& value) {
  if(_size >= _capacity){ // border check;
    cout<<"SIZE "<<_size<<" CAP "<<_capacity;
    cout << " The List is overflow!" << endl;
    return false;
  }
  _elem[_size++] = value;
}

会输出SIZE 0 CAP 2000 The List is overflow!。

看到这里，你可能已经急了。明明size是0，cap是2000，为什么if里的size >= cap会成立呢？先别急，接着看下面的代码：

3. 这段代码很难找出错（所以建议跳过去不看）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

#include <iostream>
using namespace std;
int main() {
  int n, s, m, j, tempt, q, k, flag;
  int count = 1;
  int data[2020];
  cin >> n >> s >> m;
  tempt = s;
  for (int i = 0; i < n; i++) {
    data[i] = i + 1;
  }
  for (; count <= n; count++) { // 主要看这个for循环
    for (k = 1, q = 0; k <= m; q++) {
      if (data[(tempt + q - 1) % n] != 0)
        k++;
    }
    if (count != n) {
      cout << data[(tempt + q - 2) % n];
      cout << ' ';
    } else {
      cout << data[(tempt + q - 2) % n];
      return 0;
    }
    data[(tempt + q - 2) % n] = 0;
    for (j = 1, flag = 0; flag != 1; j++) {
      if (data[(tempt + q + j - 2) % n] != 0)
        flag = 1;
      else
        flag = 0;
    }
    tempt = (tempt + q + j - 2) % n;
  }
  return 0;
}

但是，强大的Clang编译器有各种错误检查。我们编译的时候加上“未定义行为检测器”试试：

1
2
3
4
5
6

$ clang++ a.cpp -Wall --std=c++17 -fsanitize=undefined
$ ./a.out
6 1 1 // 这行是输入的
a.cpp:14:9: runtime error: index -1 out of bounds for type 'int [2020]'
SUMMARY: UndefinedBehaviorSanitizer: undefined-behavior a.cpp:14:9 in 
1 2 3 4 5 6

会发现这个代码访问了数组里下标为-1的地方。

上面的几段代码有什么共同点呢？为什么在平台上的执行结果就和本地不一样呢？为什么这几段代码表现出来好像“平台不好用了”呢？要回答这个问题，首先要理解“未定义行为”的概念。

什么是未定义行为

在我们学习编程的过程中，可能都知道一些行为是“非法”的，是“错误”的，比如：

1. 数组越界访问
2. 解引用空指针
3. 在对象的生命周期结束后访问对象
4. 有返回类型的函数没有从return结束

但是，我们也仅仅知道这些行为是“错误”的，并不会知道这些行为为什么错误，会造成哪些后果。这些行为在c++语言标准里有一个名字：未定义行为（undefined behavior）。如：

控制流出有返回值的函数（除了 main）的结尾而不经过 return 语句是未定义行为。

翻译成人话就是，除了main之外的函数，如果他有返回值但是不经过return语句就结尾了，行为未定义。

标准中也明确给出了未定义行为的解释：

• 未定义行为（undefined behavior，UB）——对程序的行为无任何限制。未定义行为的例子是数组边界外的内存访问，有符号整数溢出，空指针的解引用，在一个表达式中对同一标量多于一次的中间无序列点 (C++11 前)无序 (C++11 起)的修改，通过不同类型的指针访问对象，等等。编译器不需要诊断未定义行为（尽管许多简单情形确实会得到诊断），而且所编译的程序不需要做任何有意义的事。

甚至：

• 未定义行为能导致时间旅行（在所有事项中，时间旅行可是最惊人的）

翻译成人话就是，如果发生未定义行为，编译器可以把这段代码编译为任何内容，包括但不限于删除你的所有文件，帮你定一杯咖啡，或者时间旅行。**这些都是严格符合C++语言标准的。**同时，不同的编译器也会对未定义行为采取不同的策略，所以很可能未定义行为的代码在不同编译器上运行结果不同。这样定义”未定义行为“就使得编译器优化更好：很多情况下既然结果未定义，就可以没有结果，因此编译器可以去掉未定义行为发生的代码分支，把代码优化为行为确定的结果。

不理解上面那段话什么意思？没关系，我们回过来看之前的那段代码：

1
2
3
4
5
6
7
8

template<typename T> bool ArrayList<T>::append(T const& value) {
  if(_size >= _capacity){ // border check;
    cout<<"SIZE "<<_size<<" CAP "<<_capacity;
    cout << " The List is overflow!" << endl;
    return false;
  }
  _elem[_size++] = value;
}

这段代码中实现了一个顺序表的append方法。看上去没什么问题：由于没有实现扩容算法，在末尾插入时首先要进行边界检查。如果边界检查通过，就把value放到elem里，并size++。但是，上面说了，这段代码的运行结果是if内条件永远成立，即使后面输出的时候size为0，cap为2000。为什么会这样呢？这是不是编译器的Bug？

其实并不是。可能你已经注意到了：这个函数最后缺少return。因此，if内条件不成立的行为未定义。编译器发现了这一点，认为程序员会保证每次调用的时候if内条件都成立（否则就会出现未定义行为），因此直接去掉了if，把代码编译成了大概这个样子：

1
2
3
4
5

template<typename T> bool ArrayList<T>::append(T const& value) {
  cout<<"SIZE "<<_size<<" CAP "<<_capacity;
  cout << " The List is overflow!" << endl;
  return false;
}

重新回顾这个优化的过程中编译器的思路：

1. if内条件不成立的话，行为未定义。
2. 未定义行为不好，写代码的人会避免未定义行为。
3. 因此，写代码的人会保证每次调用的时候if内条件均成立。
4. 因此可以去掉if。

可以发现，整个优化过程中编译器严格的遵守了C++语言标准：

• 如果if内条件成立，这样的执行结果自然是正确的
• 如果if内条件不成立，那么行为未定义。既然行为未定义，那任何行为都是正确的，因此我执行if内条件成立的代码也是正确的行为。

因此，错的不是编译器，是整个世界你。编译器没那么多bug，当你以为编译器出了bug，绝大部分情况下是你写了bug。

当然，go编译器里还是不少bug的，这个之后再说

因此，到现在你应该知道了什么是未定义行为。任何包括未定义行为的代码运行结果恰好符合你的预期都是巧合。任何时候不应该写有未定义行为的代码。未定义行为会导致代码在不同平台不同编译器上运行结果不一致。

未定义行为的危害

未定义行为对于代码的危害上面已经说的差不多了。你可能会觉得：顶多代码运行结果是错的，又会怎么样呢？**NAIVE！**前面说道，当遇到未定义行为时：

编译器可以把这段代码编译为任何内容，包括但不限于删除你的所有文件，帮你定一杯咖啡，或者时间旅行。这些都是严格符合C++语言标准的。

不要以为“删除你的所有文件”是危言耸听：有人发现在clang编译器下你真的可能因为未定义行为而格式化你的硬盘：

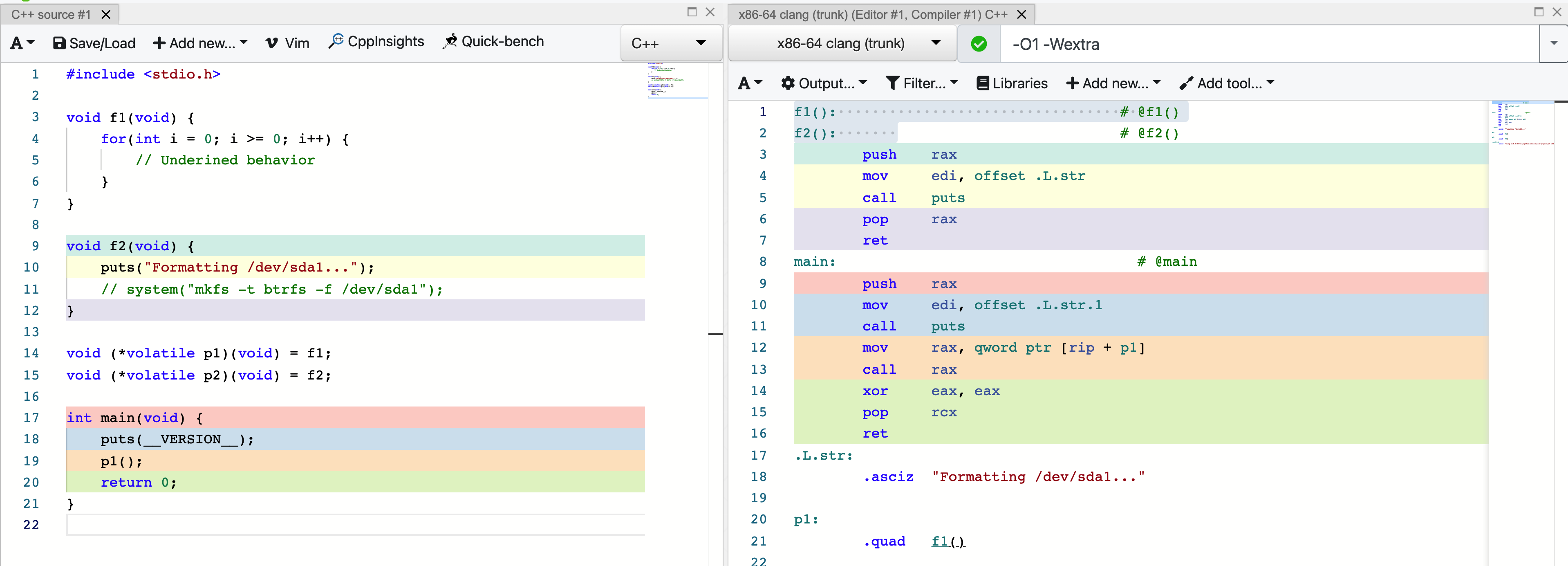
这段代码首先定义了一个函数f1。在这个函数中，i会不断累加，直到溢出。有符号数溢出是未定义行为。于是，编译器没有给f1生成任何代码，只生成了一个label。

从右侧的汇编可以看到，f1label下面的代码就是f2函数，这个函数会格式化你的硬盘（在这个例子并没有真的格式化，注释掉了。）学过汇编的同学可能会发现，由于f1内没有任何代码，所以调用f1会执行你本来不想执行的f2函数。BOOM！你的硬盘被格式化了。

在llvm的issue tracker中有关这个 “bug”的讨论还在进行中。一部分人认为应该“修复”：

This means UB is a potential safety/security problem, and we really should do something about it.

还有一部分人认为不应该：

All sorts of UB manifests in lots of security issues, right? Buffer overruns and the like (I guess this is a buffer overrun, of sorts).

同时，有些人认为应该修复，理由是为了debug更方便。llvm的开发者回复：

It’s not generally that simple - deciding where/how to “recover” from UB would be pretty difficult.

The Clang-advised way to deal with this would be to compile with -fsanitize=undefined

https://godbolt.org/z/3aW69c

example.cpp:4:29: runtime error: signed integer overflow: 2147483647 + 1 cannot be represented in type ‘int’
SUMMARY: UndefinedBehaviorSanitizer: undefined-behavior example.cpp:4:29 in

大意是已经有足够强大的未定义行为检测器了，为了方便debug来改这个UB的行为不值得。

总之，不要写未定义行为，以及当你以为编译器错了，你错了。我的OJ同理，因为就是帮你调用编译器来编译代码而已…

个人题解，和比赛官方无关，仅供参考

2020工大杯题解 - E - Lawn Pattern Design

题目描述

Mr. Leo is a famous computer scientist, he invited you and your classmates to go on a vacation in his new house in the mountains. After a day of playing, many of you felt comfortable and sighed: “It’s quite nice to live in the mountains!”. Mr. Leo agreed with that, and he decided to play a game with you, to make the travel even more interesting.

There is an unmaintained lawn next to Mr. Leo’s house, he let you design a pattern for this lawn, and submit the pattern with a computer program. The lawn is 5 meters wide and 12 meters long, you are supposed to take one square meter as one unit, use “g” to indicate grass, and use “.” to indicate bare ground. For example, an unmaintained lawn can be described as the following:

1
2
3
4
5
6
7
8
9
10
11
12

.gggg
ggggg
gg.gg
ggggg
g..gg
ggggg
ggggg
ggggg
ggggg
ggggg
gggg.
gggg.

You had no idea about the pattern. However, your friend classmate T came to encourage and team up with you. “No matter what difficulties we meet, don’t be afraid, face it with a smile!” classmate T said, “Because the best way to overcome fear is to face it. Come on!”. After listening to the encouraging speech, you felt confident and asked him what could you do to help him. Classmate T explains that he had always believed that nobody knows pattern design better than him, however, he knew nothing about computer science. So he needed you to write his program to output his wonderful design.

You accepted the task at once, and ask him when can you get the final design. classmate T said that good designs need time to perfect, and he needs to find a great way to inform the Chinese character element in his design. Just like he always says: “Normal pretty design, not ok. Pretty design with Chinese character element, ok!”. After a night of work, classmate T finally gave you his design, please write a program to output it.

classmate T’s design:

1
2
3
4
5
6
7
8
9
10
11
12

.g.g.
ggggg
.g.g.
ggggg
g...g
ggggg
g...g
ggggg
..g..
ggggg
..g..
..g..

Input

There isn’t any input for this problem.

Output

Output classmate T’s design.

题解

题目重述

逗比题，直接输出即可。

用草字拼个草。

题目解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

#include <iostream>
using namespace std;
int main(){
    cout<<".g.g.\n"
          "ggggg\n"
          ".g.g.\n"
          "ggggg\n"
          "g...g\n"
          "ggggg\n"
          "g...g\n"
          "ggggg\n"
          "..g..\n"
          "ggggg\n"
          "..g..\n"
          "..g..\n";
    return 0;
}

彩蛋：

c / c++ 语言中， 如果两个字符串挨着， 中间没有代码， 如上面样例一样，就会合并为一个字符串。

**个人题解，和比赛官方无关，仅供参考

2020工大杯题解 - F - L 同学的程序课

题目描述

上完体育课之后，L同学接下来要上程序课。程序课自然离不开写代码，而写代码也离不开修BUG。虽然L同学十分优秀，但是也难逃与BUG斗争的命运。

所幸，L同学在与BUG的长时间较量中，积累了不少的经验。他发现他的程序可能出现的BUG共有N种。对于这些BUG，L同学掌握了K种方法，每种方法可以彻底修复一个$A_i$类BUG，这需要花费$T_{1i}$的时间。

但对于大部分BUG而言彻底修复是很困难的，在修复的过程中往往会产生一个新的BUG。对此，L同学还掌握了M种方法，每种方法可以修复一个$B_j$类BUG，但同时会产生一个$C_j$类BUG，这需要花费$T_{2j}$的时间。

现在，为了能尽快的完成程序课作业，L同学希望能够知道使用他目前所掌握的方法，彻底修复一个第x类BUG所需要的最短时间是多少。由于L同学学业繁忙，所以只能由你来帮助他了。

输入

第一行，三个整数N、K、M，分别代表一共有N种BUG（BUG的编号从1到N）、L同学掌握K种能够彻底修复一个BUG的方法，和M种在产生一个新BUG的情况下修复一个BUG的方法。

而后K行，每行两个整数$A_i$、$T_{1i}$，代表L同学掌握一种方法能够用$T_{1i}$的时间彻底修复一个$A_i$类BUG。

而后M行，每行三个整数$B_j$、$C_j$、$T_{2j}$，代表L同学掌握一种方法能够用$T_{2j}$的时间将一个$B_j$类BUG修复，但同时会产生一个$C_j$类BUG。

输出

共一行，用空格隔开的N个整数，第x个整数代表使用L同学使用掌握的方法彻底修复一个第x类BUG需要的最短时间。特别地，如果使用现有的方法无法彻底修复第x类的BUG，请在对应位置输出”INF”。

数据规模

对于100%的数据有：

$1 \leq N \leq 10^5$

$0 \leq K,M \leq 2*10^5$

$0 \leq K+M \leq 2*10^5$

$1 \leq A_i,B_j,C_j \leq N$

$1 \leq T_{1i},T_{2j} \leq 10^4$

$1 \leq \sum_{i=1}^{K}T_{1i}+\sum_{j=1}^{M}T_{2j} \leq 10^9$

输入输出样例

Input

1
2
3
4
5
6
7
8

5 3 4
1 3
2 9
5 1
1 3 4
4 2 5
1 2 2
2 5 3

Output

1

3 4 INF 9 1 

题解

题目解法

可以把 bug 视为一个图：有一个虚拟的 0 号节点代表彻底修复的 bug。如果第 $i$ 个 bug 可以转变为 $j$ 类 bug ，则由 $j$ 连接到 $i$ 一条单向边，权重为所需时间。如果可以彻底修复第$i$类 bug，则由 $0$ 连接到 $i$ 一条单向边，权重为所需时间。然后求 $0$ 号节点到每个节点的最短路即可。

分析时间复杂度：$1 \leq N \leq 10^5$ $0 \leq K,M \leq 2*10^5$ 因此使用堆优化的 $dijkstra$ （时间复杂度为$O\left(m \times \log\left(m\right)\right)$）即可。

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
#define MAXN 100050
struct road{
    int from;
    int time;
    road(int from, int time): from(from), time(time){}
    bool operator>(const road& that) const {
        return time > that.time;
    }
};
vector<road> roads[MAXN];
int dji[MAXN] = {0x3fffffff};
int vis[MAXN] = {0};
int n,k,m;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>n>>k>>m;
    int t,a,b;
    for(int i = 0; i < k; ++ i){
        cin>>a>>b;
        roads[0].emplace_back(a, b);
    }
    for(int i = 0; i < m; ++ i){
        cin>>a>>b>>t;
        roads[b].emplace_back(a, t);
    }

    int count = 0;
    priority_queue<road, vector<road>, greater<road> > que;
    for(int i = 1; i <= n; ++ i){
        dji[i] = 0x3fffffff;
        vis[i] = 0;
    }
    dji[0] = 0;
    que.emplace(0,0);
    while(!que.empty()){
        int from = que.top().from;
        que.pop();
        if(vis[from]){
            continue;
        }
        vis[from] = 1;
        for(auto &rr: roads[from]){
            if (dji[rr.from] > rr.time + dji[from]){
                dji[rr.from] = rr.time + dji[from];
                que.emplace(rr.from, dji[rr.from]);
            }
        }
        count++;
        if(count == n+1) break;
    }

    for(int i = 1; i <= n; ++ i){
        if(dji[i] < 0x3fffffff){
            cout<<dji[i]<<" ";
        } else {
            cout<<"INF ";
        }
    }
    return 0;
}

个人题解，和比赛官方无关，仅供参考

2020工大杯题解-G - L 同学的睡眠

题目描述

L同学日理万机，睡眠非常不规律，最早下午7点就会睡觉，最晚早上7点才去睡觉。但规律的睡眠才会使L同学精力充沛，善良的你快关心一下L同学吧！

输入

第一行为空格分隔的3个整数$N,D,T$。在接下来的$N$天里，细心的你将记录L同学每天的睡眠时间，从第2天开始，如果在你所记录的过去$D$天内(包括当天)L同学最早和最晚睡眠时间差超过了$T$分钟，那么善良的你需要对L同学说句“辛苦了！”。

第二行为空格分隔的$N$个时间，依次表示$1\sim
N$天你所记录L同学的睡眠时间，采用HH:MM格式的24小时制表示。

$2\le N \le 10^5, 2 \le D \le 10^5, 1 \le T \le 719$

输出

输出一个整数表示你一共需要对L同学说多少次“辛苦了！”

样例输入

1
2

5 3 30
23:30 1:20 1:07 0:50 19:00

样例输出

1

3

题解

题目重述

$2\le N \le 10^5, 2 \le D \le 10^5, 1 \le T \le 719$

暴力查询的时间复杂度为 $O(D \times N)$，肯定是不行的。因此，需要一种区间最值查询的数据结构。因此，这是一个 RMQ 问题。

RMQ 是英文 Range Maximum/Minimum Query 的缩写，表示区间最大（最小）值。

可以使用线段树、ST 表、单调栈解决问题。由于线段树和单调栈太简单了，没意思，这里介绍 ST 表。

ST 表是用于解决 可重复贡献问题 的数据结构。

可重复贡献问题 是指对于运算 ，满足 ，则对应的区间询问就是一个可重复贡献问题。例如，最大值有 ，gcd 有 ，所以 RMQ 和区间 GCD 就是一个可重复贡献问题。像区间和就不具有这个性质，如果求区间和的时候采用的预处理区间重叠了，则会导致重叠部分被计算两次，这是我们所不愿意看到的。另外， 还必须满足结合律才能使用 ST 表求解。

ST 表基于 倍增 思想，可以做到 $\Theta(n\log n)$ 预处理， $\Theta(1)$ 回答每个询问。但是不支持修改操作。

基于倍增思想，我们考虑如何求出区间最大值。可以发现，如果按照一般的倍增流程，每次跳 $2^i$ 步的话，询问时的复杂度仍旧是 $\Theta(\log n)$ ，并没有比线段树更优，反而预处理一步还比线段树慢。

我们发现 $\max(x,x)=x$ ，也就是说，区间最大值是一个具有“可重复贡献”性质的问题。即使用来求解的预处理区间有重叠部分，只要这些区间的并是所求的区间，最终计算出的答案就是正确的。

如果手动模拟一下，可以发现我们能使用至多两个预处理过的区间来覆盖询问区间，也就是说询问时的时间复杂度可以被降至 $\Theta(1)$ ，在处理有大量询问的题目时十分有效。

具体实现如下：

令 $f(i,j)$ 表示区间 $[i,i+2^j-1]$ 的最大值。

显然 $f(i,0)=a_i$ 。

根据定义式，第二维就相当于倍增的时候“跳了 $2^j-1$ 步”，依据倍增的思路，写出状态转移方程： $f(i,j)=\max(f(i,j-1),f(i+2^{j-1},j-1))$ 。

以上就是预处理部分。而对于查询，可以简单实现如下：

对于每个询问 $[l,r]$ ，我们把它分成两部分： $f[l,l+2^s-1]$ 与 $f[r-2^s+1,r]$ 。

其中 $s=\left\lfloor\log_2(r-l+1)\right\rfloor$ 。

根据上面对于“可重复贡献问题”的论证，由于最大值是“可重复贡献问题”，重叠并不会对区间最大值产生影响。又因为这两个区间完全覆盖了 $[l,r]$ ，可以保证答案的正确性。

以上内容以 CC BY-SA 4.0 协议和 SATA 协议提供在 OI-WIKI。

贡献者：orzAtalod, Henry-ZHR, leoleoasd, Chrogeek, H-J-Granger, ouuan

题目解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

#include <iostream>
using namespace std;
const int logn = 17;
const int maxn = 100050;
int fmax[maxn][logn+1], fmin[maxn][logn+1], Logn[maxn];
void pre() {
    Logn[1] = 0;
    Logn[2] = 1;
    for (int i = 3; i < maxn; i++) {
        Logn[i] = Logn[i / 2] + 1;
    }
}
int querymax(int x,int y){
    return max(fmax[x][Logn[y - x + 1]], fmax[y - (1 << Logn[y - x + 1]) + 1][Logn[y - x + 1]]);
}
int querymin(int x,int y){
    return min(fmin[x][Logn[y - x + 1]], fmin[y - (1 << Logn[y - x + 1]) + 1][Logn[y - x + 1]]);
}
int main() {
    cin.tie(nullptr);
    ios::sync_with_stdio(false);
    int n,d,t;
    int a,b;
    int output = 0;
    char _;
    cin>>n>>d>>t;
    for (int i = 1; i <= n; i++){
        cin>>a>>_>>b;
        fmax[i][0] = (a + 5) % 24 * 60 + b;
        fmin[i][0] = (a + 5) % 24 * 60 + b;
    }
    pre();
    for (int j = 1; j <= logn; j++)
        for (int i = 1; i + (1 << j) - 1 <= n; i++){
            fmax[i][j] = max(fmax[i][j - 1], fmax[i + (1 << (j - 1))][j - 1]);
            fmin[i][j] = min(fmin[i][j - 1], fmin[i + (1 << (j - 1))][j - 1]);
        }

    for (int i = 1; i <= n; ++ i){
        int mm = querymax( max(i - d + 1, 1), i);
        int mi = querymin( max(i - d + 1, 1), i);
        if (mm - mi  > t){
            output++;
        }
    }
    cout<<output<<endl;
    return 0;
}

个人题解，和比赛官方无关，仅供参考

2020工大杯题解 - D - L 同学的又一节体育课

题目描述

迫于忘了选体育课, L同学只能上一个没人选的奇怪的体育课. 在这门课上,
学生被要求玩一个奇怪的游戏, 叫做 “能量传输”. 在这个游戏中, 同学们的目标是组成轨道,
把球从起点传输至筒中, 并保证全程球不能脱轨, 不能把筒撞倒. 全班同学被分成两组, 分别比赛,
之后老师会根据完成小组完成任务的时间的排名来赋予平时分. L同学想要在体育课上内卷,
他想知道需要卷到什么程度. 他偷偷瞄到了另一个组的轨道,
想要问问你另一个组需要多久来完成任务.

一个轨道可以视为一个 8 个长度为 16 的字符串, 如下表示:

1
2
3
4
5
6
7
8

-
 \
  \
   -----
        \
         \  --
          -/  \
               V

• - 表示一个横着摆放的轨道.
• / 和 \ 分别表示 上升/下降 的斜着摆放的轨道.
• V 表示目标球桶.
• 行末最后的空格 可以省略. 如, 上面的字符矩阵中的第一行, 右边省略了15个空格.

为了模拟球的行为, 我们可以认为球有以下属性:

• 坐标 $\left(x,y\right)$. $x$表示横坐标,$y$表示高度. $1 \leq x \leq 16, 1 \leq y \leq 8$。
  左下角坐标为$\left(1,1\right)$, $x$正方向向上, $y$正方向向右.
• 速度 v. 不考虑速度的矢量性.

不同摆放的轨道会对于球的速度有如下影响:

• -: v -= 3
• \: v += 10
• /: v -= 15

在运球过程中, 有以下限制:

• 任意时刻, 球的速度不能超过40, 否则会冲出轨道外.
• 任意时刻, 球的速度不能小于或等于0, 否则会停止运动.
• 落入桶中的时候, 球的速度不能超过15, 不然会把桶撞倒.

我们定义球的一次移动为球的横坐标加一的过程. 在球的一次移动中:

• 如果当前轨道是 \:
  • 如果下一个轨道是 \: 其高度必须比当前轨道少1.
  • 如果下一个轨道是 /: 其高度必须比当前轨道少1.
  • 如果下一个轨道是 -: 其高度必须比当前轨道少1.
  • 如果下一个轨道是 V: 其高度必须比当前轨道少1.
• 如果当前轨道是 -:
  • 如果下一个轨道是 \: 其高度必须比当前轨道少1.
  • 如果下一个轨道是 /: 其高度必须和当前轨道相同.
  • 如果下一个轨道是 -: 其高度必须和当前轨道相同.
  • 如果下一个轨道是 V: 无论高度如何, 球会脱轨.
• 如果当前轨道是 /:
  • 如果下一个轨道是 \: 无论高度如何, 球会脱轨.
  • 如果下一个轨道是 /: 其高度必须比当前轨道多1.
  • 如果下一个轨道是 -: 其高度必须比当前轨道多1.
  • 如果下一个轨道是 V: 无论高度如何, 球会脱轨.

为了简化问题, 我们可以如下进行模拟:

1. 球的初速度为4.
2. 如果当前轨道是V: 则已经到达终点. 跳转到第六步.
3. 把通过当前轨道所需时间 $30 / v$ 累加到总时间中. 做除法后保留整数部分.
4. 通过轨道后, 根据轨道类型, 更新当前速度, 并判断是否可以进入下一个轨道.
5. 跳转到第二步.
6. 输出完成任务所需要的总时间. 如果不能完成任务, 请输出-1.

球的初始坐标为 (1, 8), 保证这一格的轨道为 -. 保证坐标为$\left(16, 1\right)$的地方的轨道为V.

输入数据

8 行, 每行一个长度为 16 的字符串, 表示轨道.

保证每列只有一个不是空格的字符, 且其属于 / \ - V

输出数据

一个整数, 代表和 L 同学竞争的组完成任务所需时间.

如果不能完成任务, 请输出-1.

样例输入

1
2
3
4
5
6
7
8

-
 \
  \
   -----
        \
         \  --
          -/  \
               V

样例输出

1

80

样例解释

通过每一格的速度分别为:

4 1 11 21 18 15 12 9 6 16 26 23 8 5 2

所需时间分别为

7 30 2 1 1 2 2 3 5 1 1 1 3 6 15

题解

题目重述

大模拟题，暴力模拟即可，考察细节。

题目解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111

#include <iostream>
#include <string>
using namespace std;

int main(){
    int height[17] = {0};
    int type[17] = {0};
    // -: 0  /: 1 \: 2 v: 3
    int delta_V[4] = {-3,-15,10,0};
    string now;
    for(int i = 0; i < 8; ++ i){
        getline(cin, now);
        int j = 0;
        for(char &c: now){
            switch(c){
                case '-':
                    height[j+1] = 8 - i;
                    type[j+1] = 0;
                    break;
                case '/':
                    height[j+1] = 8 - i;
                    type[j+1] = 1;
                    break;
                case '\\':
                    height[j+1] = 8 - i;
                    type[j+1] = 2;
                    break;
                case 'V':
                    height[j+1] = 8 - i;
                    type[j+1] = 3;
                    break;
                default:
                    break;
            }
            j++;
        }
    }
    int v = 4;
    int x = 1;
    int y = 8;
    int t = 0;
    while(true){
        //cout<<v<<" ";
        if(type[x] == 3){
            if(v > 15){
                t = -1;
            }
            break;
        }
        if(v > 40 or v <= 0){
            t = -1;
            break;
        }
        t += (30 / v);
        if(type[x] == 0){
            if(type[x+1] == 0){
                if(height[x+1] != height[x]){
                    t = -1;
                    break;
                }
            }else if(type[x+1] == 1){
                if(height[x+1] != height[x]){
                    t = -1;
                    break;
                }
            }else if(type[x+1] == 2){
                if(height[x+1] != height[x]-1){
                    t = -1;
                    break;
                } else {
                    y -= 1;
                }
            }else if(type[x+1] == 3) {
                t = -1;
                break;
            }
        }else if(type[x] == 1) {
            if(type[x+1] == 0) {
                if(height[x+1] != height[x] + 1){
                    t = -1;
                    break;
                } else {
                    y += 1;
                };
            }else if(type[x+1] == 1) {
                if(height[x+1] != height[x] + 1){
                    t = -1;
                    break;
                } else {
                    y += 1;
                };
            }else if(type[x+1] == 2) {
                t = -1;
                break;
            }else if(type[x+1] == 3){
                t = -1;
                break;
            }
        }else if(type[x] == 2) {
            if(height[x+1] != height[x] - 1){
                t = -1;
                break;
            }
            y -= 1;
        }
        v += delta_V[type[x]];
        x++;
    }
    cout<<t<<endl;
    return 0;
}